Derivación en Cadena
Descripción de la regla
En términos intuitivos, si una variable y, depende de una segunda variable u, que a la vez depende de una tercera variable x; entonces, la razón de cambio de y con respecto a x puede ser computado como el producto de la razón de cambio de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.
Descripción algebraica
En boxes los términos algebraicos, la regla de la cadena (para funciones de una variable) afirma que si  es diferenciable en
es diferenciable en  y
y  es una función diferenciable en
es una función diferenciable en  , entonces la función compuesta
, entonces la función compuesta 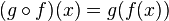 es diferenciable en
es diferenciable en  y
y
 es diferenciable en
es diferenciable en  y
y  es una función diferenciable en
es una función diferenciable en  , entonces la función compuesta
, entonces la función compuesta 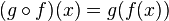 es diferenciable en
es diferenciable en  y
y
Notación de Leibniz
Alternativamente, en la notación de Leibniz, la regla de la cadena puede expresarse como:
donde  indica que g depende de f como si ésta fuera una variable.
indica que g depende de f como si ésta fuera una variable.
 indica que g depende de f como si ésta fuera una variable.
indica que g depende de f como si ésta fuera una variable.Ejemplo conceptual
Supóngase que se está escalando una montaña a una razón de 0,5 kilómetros por hora. La razón a la cual la temperatura decrece es 6 °F por kilómetro (la temperatura es menor a elevaciones mayores). Al multiplicar 6 °F por kilómetro y 0,5 kilómetros por hora, se obtiene 3 °F por hora, es decir, la razón de cambio de temperatura con respecto al tiempo transcurrido.
Este cálculo es una aplicación típica de la regla de la cadena.
Ejemplo algebraica
Por ejemplo si y = f(u) es una función derivable de u y si además u = g(x) es una función derivable de x entonces y = f(g(x)) es una función derivable con:
o también
Ejemplo 1
y queremos calcular:
Por un lado tenemos:
y
si:
entonces:
Si definimos como función de función:
resulta que:
con el mismo resultado.
Derivación implícita
Es posible derivar una función dada implícitamente sin necesidad de expresarlo explícitamente. El método consiste en derivar los dos miembros de la relación. El procedimiento se conoce como derivación implícita.
Definición: se denomina función implícita cuando se da una relación entrex yy por medio de una ecuación no resuelta paray, entoncesy se llama función implícita dex.
.



![\frac{d}{dx} [f(g(x))]=f '(g(x))\cdot g'(x)](http://upload.wikimedia.org/math/8/5/8/858ff94f3748b67089b3b3a0f4048bcf.png)

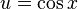
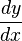




No hay comentarios:
Publicar un comentario